The Fourth Dimension
GA 324a
24 March 1905, Berlin
Translated by Steiner Online Library
First Lecture
If you are disappointed about what you are about to hear, I would like to say in advance that today I want to discuss very elementary things [about the fourth dimension]. Those who want to delve deeper into this question should be very familiar with the higher concepts of mathematics. I would like to give you some very elementary and general concepts. One must distinguish between the possibility of thinking in a four-dimensional space and reality. Whoever is able to make observations there is dealing with a reality that extends far beyond what we know as the sensual-real. You have to do thought transformations when you go there. You have to let things play into mathematics a little, find your way into the way of thinking of the mathematician.
You have to realize that the mathematician does not take a step without accounting for what arrives at his conclusions. But we must also realize when we deal with mathematics that even the mathematician cannot penetrate a single step [into reality], that he cannot draw any conclusions [that go beyond what is merely possible in thought]. First of all, it is about simple things, but they become more complicated when one wants to arrive at the concept of the fourth dimension. We must be clear about what we mean by dimensions. It is best to examine the various spatial structures in terms of their dimensionality. They lead to considerations that were only tackled in the 19th century by great mathematicians such as Bolyai, Gauss and Riemann.
The simplest spatial size is the point. It has no extension at all; it must be conceived. It is the fixation of an extension in space. It has no dimension. The first dimension is the line. The straight line has one dimension, length. If we move the line, which has no thickness, ourselves, we step out of the one dimension, and the line becomes a surface. This has two dimensions, a length and a width. If we move the surface, we step out of these two dimensions and we get the body. It has three dimensions: height, width, depth (Figure 1).
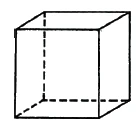
If you move the body itself, if you move a cube around in space, you will again only get a spatial body. You cannot move space out of itself.

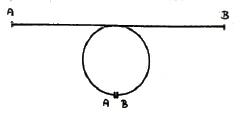
We need to turn to a few other concepts. If you look at a straight line, it has two boundaries, two endpoints A and B (Figure 2).
Let's imagine that we want A and B to touch. But if they are to touch, we have to curve the line. What happens? You cannot possibly remain within the [one-dimensional] line if you want to make A and B coincide. To connect points A and B, we have to step out of the straight line itself, we have to step out of the first dimension and into the second dimension, the plane. In this way, the straight line becomes a closed curve (that is, in the simplest case, a circle) by bringing its endpoints into alignment (Figure 3).
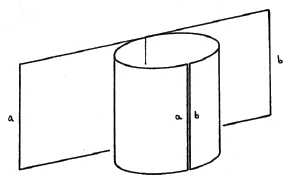
It is therefore necessary to go beyond the first dimension; you cannot remain within it. Only in this way can the circle be created. You can perform the same operation with a surface. However, this only works if you do not remain within the two dimensions. You have to enter the third dimension and then you can turn the surface into a tube, a cylinder. This operation is done in a very similar way to the way we brought two points into coincidence earlier, thereby moving out of the first dimension. Here, in order to bring two boundaries of the surface into coincidence, we have to move into the third dimension (Figure 4).
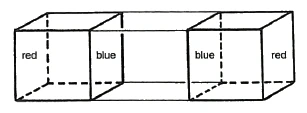
Is it conceivable that a similar operation could be carried out with a spatial structure that already has three dimensions itself? If you have two congruent cubes, you can slide one into the other. [Now imagine two congruent cubes as the boundaries of a three-dimensional prismatic body.] If you try to make one cube, which is colored red on one side [and blue on the opposite side], fit exactly over the other cube, which is otherwise [geometrically] identical but with the red and blue colors swapped, then you cannot make them fit except by rotating the cube (Figure 5).
Let us consider another spatial structure. If you take the left-hand glove, it is impossible for you to pull the left-hand glove over the right hand. But if you look at the two [mirror-symmetrical] gloves together, like the straight line with the end points A and B, you have something that belongs together. It is then a single entity, with a boundary [that is, with a mirror plane] in the middle. It is very similar with the two symmetrical halves of the human outer skin. 2
How can we now make two [mirror] symmetrical three-dimensional structures coincide? Only if we go beyond the third dimension, as we did with the first and second. We can also put the right or left glove over the left or right hand, respectively, when we walk through four-dimensional space.
[When constructing the third dimension (depth dimension) of the visualization space, we align the image of the right eye with that of the left eye and place it over it.
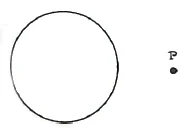
We now look at an example from Zöllner. We have a circle and a point P outside of it. How can we bring the point P into the circle without crossing the circle? This is not possible if we remain within the plane. Just as one has to go from the second dimension into the third when moving from a square to a cube, we also have to go out of the second dimension here. With a sphere, there is also no possibility of entering [into the interior] without [piercing the surface of the sphere or] going beyond the third dimension.
These are possibilities for thought, but they have a practical significance for the theory of knowledge, [in particular for the problem of the objectivity of the content of perception]. If we realize how we actually perceive, we will come to the following view. Let us first ask ourselves: How do we gain knowledge of bodies through our senses? We see a color. Without eyes, we would not perceive it. The physicist then says: Out there in space is not what we call color, but purely spatial forms of movement; they penetrate through our eye, are captured by the optic nerve, transmitted to the brain, and there, for example, the red arises. One may now ask: Is the red also present when there is no sensation?
Red could not be perceived without the eye. The ringing of a bell could not be perceived without the ear. All our sensations depend on the transformation of forms of motion by our physical and mental apparatus. However, the matter becomes even more complicated when we ask ourselves: Where is the red, this peculiar quality, actually located? Is it in the body? Is it a process of vibration? Outside there is a process of movement, and this continues right into the eye and into the brain itself. There are vibrational [and nervous] processes everywhere, but red is nowhere to be found. Even if you examine the eye, you would not find red anywhere. It is not outside, but it is also not in the brain. We only have red when we, as a subject, confront these processes of movement. So do we have no possibility at all to talk about how the red meets the eye, how a c sharp meets the ear?
The question is, what is this inner [representation], where does it arise? In the philosophical literature of the 19th century, you will find that this question runs through everything. Schopenhauer, in particular, has provided the following definition: The world is our representation. But what then remains for the external body? [Just as a color representation can be “created” by movements, so can] movement can arise in our inner self through something that is basically not moved. Let us consider twelve snapshots of a [moving] horse figure on [the inside of] a [cylinder] surface, [which is provided with twelve fine slits in the spaces between. If we look at the rotating cylinder from the side,] we will have the impression that it is always the same horse and that only its feet are moving. So [the impression of] movement can also arise through our [physical organization] when something is not moving at all [in reality]. This is how we arrive at a complete dissolution of what we call movement.
But what then is matter? If you subtract color, movement [shape, etc., i.e. what is conveyed by sensory perception] from matter, then nothing remains. If we already have the [secondary, i.e. “subjective” sensations [color, sound, warmth, taste, smell] within us, we must also place [the primary sensations, that is, shape and movement,] within us, and with that the external world completely disappears. However, this results in major difficulties [for the theory of knowledge].
Let us assume that everything is outside, how then do the properties of the object outside come into us? Where is the point [where the outside merges into the inside]? If we subtract all [sensory perceptions], there is no outside anymore. In this way, epistemology puts itself in the position of Münchhausen, who wants to pull himself up by his own hair. But only if we assume that there is an outside, only then can we come to [an explanation of] the sensations inside. How can something from the outside enter our inside and appear as our imagination?
We need to pose the question differently. Let us look at some analogies first. You will not be able to find a relationship [between the outside world and the sensation inside] unless you resort to the following. We return to the consideration of the straight line with endpoints A and B. We have to go beyond the first dimension, curve the line, to make the endpoints coincide (Figure 7).
Now imagine the left endpoint A [of this straight line] brought together with the right endpoint B so that they touch at the bottom, so that we are able to return to the starting point [via the coinciding endpoints]. If the line is small, the corresponding circle is also small. If I turn the [initially given] line into a circle and then turn larger and larger lines into circles, the point at which the endpoints meet moves further and further away from the [original] line and goes to infinity.
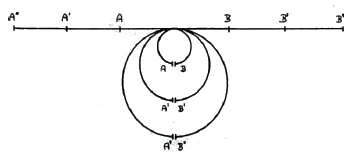
of the [original] line and goes to infinity. Only at infinity do the [increasingly large] circle lines have their endpoint. The curvature becomes weaker and weaker, and eventually we will not be able to distinguish the circle line from the straight line with the naked eye (Figure 8).
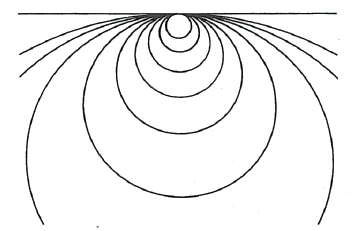
In the same way, when we walk on the Earth, it appears to us as a straight piece, although it is round. If we imagine that the two halves of the straight line extend to infinity, the circle actually coincides with the straight line.
The straight line can be conceived as a circle whose diameter is infinite.
Now, however, we can imagine that if we go through [the straight line and] remain within the line, we will come back from the other side of infinity. But in doing so, we have to go through infinity.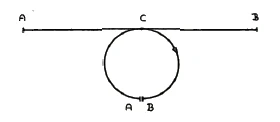
Now, instead of a [geometric] line, imagine something that is real and that connects to a reality. Let us imagine that as the point C [on the circumference of the circle] progresses, cooling occurs, that the point becomes colder and colder the further it moves away [from its starting point] (Figure 9). Let us leave the point within the circle for the time being, and, as it becomes colder and colder, let it reach the lower limit A, B. When it returns on the other side, the temperature increases again. So on the way back, the opposite condition to the one on the way there occurs. The warming increases until the temperature at C is reached again, from which we started. No matter how extended the circle is, it is always the same process: a flow of heat out and a flow of heat in. Let us also imagine this with the [infinitely extended straight] line: as the temperature [on one side increasingly] dissipates, it can rise on the other side. We have here a state that dissipates on one side while it rebuilds on the other.
In this way, we bring life and movement into the world and approach what, in a higher sense, we can call an understanding of the world. We have here two states that are interdependent and interrelated. However, for everything you can observe [sensually], the process that goes, say, to the right has nothing to do with the one that comes back from the left, and yet they are mutually dependent.
We now compare the body of the external world with the state of cooling and, in contrast, our inner sensation with the state of warming. [Although the external world and inner sensation have nothing directly perceptible in common,] they are related to each other, mutually dependent [in an analogous way to the processes described above]. This results in a connection between the external world [and our internal world] that we can support with an image: [through the relationship between] the seal and the sealing wax. The seal leaves behind an exact imprint, an exact reproduction of the seal in the sealing wax, without the seal remaining in the sealing wax [and without any material from the seal being transferred to the sealing wax]. So in the sealing wax there remains a faithful reproduction of the seal. It is quite the same with the connection between the outside world and inner sensations. Only the essential is transferred. One state determines the other, but nothing (material) is transferred.
If we imagine that this is the case with [the connection between the] outside world and our impressions, we come to the following. [Geometric] mirror images in space behave like gloves from the left and right hand. [In order to relate these directly and continuously to each other,] we have to use a new dimension of space to help us. [Now the outside world and the inner impression behave analogously to geometric mirror images and can therefore only be directly related to each other through an additional dimension.] In order to establish a relationship between the outside world and inner impressions, we must therefore go through a fourth dimension and be in a third element. We can only seek the common ground [of the outside world and inner impressions] where we [are one] with them. [One can imagine these mirror images as] floating in a sea, within which we can align the mirror images. And so we come [initially in thought] to something that transcends three-dimensional space and yet has a reality. We must therefore bring our spatial ideas to life.
Oskar Simony has tried to represent these animated spatial structures with models. [As we have seen, one comes] from the consideration of the zero-dimensional [step by step] to the possibility of imagining four-dimensional space. [On the basis of the consideration of mirror-symmetrical bodies, that is, with the help of] symmetries, we can first [most easily] recognize this space. [Another way to study the peculiarities of empirical three-dimensional space in relation to four-dimensional space is to study the knotting of curves and ribbons.] What are symmetry conditions? By intertwining spatial structures, we cause certain complications. [These complications are peculiar to three-dimensional space; they do not occur in four-dimensional spaces.]
Let's do some practical thinking exercises. If we cut a band ring in the middle, we get two such rings. If we now cut a band whose ends have been twisted by 180° and then glued, we get a single twisted ring that does not disintegrate. If we twist the ends of the tape 360° before gluing them together, then when we cut it, we get two intertwined rings. Finally, if we twist the tape ends 720°, the same process results in a knot.
Anyone who reflects on natural processes knows that such convolutions occur in nature; [in reality,] such intertwined spatial structures are endowed with forces. Take, for example, the movement of the Earth around the Sun, and then the movement of the Moon around the Earth. It is said that the Moon describes a circle around the Earth, but [if you look more closely] it is a line that is wrapped around [a circle, the orbit of the Earth], thus a helix around a circular line. And then we have the sun, which rushes through space so fast that the moon makes an additional spiral movement around it. So there are very complicated lines of force extending in space. We have to realize that we are dealing with complicated concepts of space that we can only grasp if we do not let them become rigid, if we have them in a fluid state.
Let us recall what has been said: the zero-dimensional is the point, the one-dimensional is the line, the two-dimensional the surface and the three-dimensional the body. How do these concepts of space relate to each other?
Imagine you are a creature that can only move along a straight line. What would the spatial perceptions of such a being, which itself is only one-dimensional, be like? It would not perceive its own one-dimensionality, but would only imagine points. This is because, if we want to draw something on a straight line, there are only points on the straight line. A two-dimensional being could encounter lines, and thus distinguish one-dimensional beings. A three-dimensional being, such as a cube, would perceive the two-dimensional beings. Man, then, can perceive three dimensions. If we reason correctly, we must say to ourselves: Just as a one-dimensional being can only perceive points, as a two-dimensional being can only perceive one dimension, and a three-dimensional being can only perceive two dimensions, so a being that perceives three dimensions can only be a four-dimensional being. The fact that a human being can define external beings in three dimensions, can [deal with] spaces of three dimensions, means that he must be four-dimensional. And just as a cube can only perceive two dimensions and not its third, it is true that the human being cannot perceive the fourth dimension in which he lives.
Erster Vortrag
Wenn Sie enttäuscht sein sollten über das, was Sie jetzt hören werden, will ich vorausschicken, daß ich heute ganz elementare Dinge [über die vierte Dimension] besprechen will. Wer tiefer eindringen will in diese Frage, müßte mit den höheren Begriffen der Mathematik genau bekannt sein. Ich möchte Ihnen einige ganz elementare und allgemeine Begriffe geben. Man muß unterscheiden zwischen der Möglichkeit zu denken in einem vierdimensionalen Raum und der Wirklichkeit. Wer imstande ist, dort Beobachtungen zu machen, hat es mit einer Wirklichkeit zu tun, die weit hinausreicht über das, was wir als das Sinnlich-Wirkliche kennen. Man muß Gedankenumformungen machen, wenn man sich hierher begibt. Sie müssen die Dinge ein wenig in die Mathematik hineinspielen lassen, sich hineinfinden in die Denkweise des Mathematikers.
Man muß sich klarwerden, daß der Mathematiker keinen Schritt tut, ohne sich Rechenschaft zu geben von dem, was in seinen Schlußfolgerungen eintrifft. Wir müssen aber auch gewahr werden, wenn wir uns mit Mathematik beschäftigen, daß selbst der Mathematiker keinen Schritt [in die Wirklichkeit] vordringen kann, daß er keine Schlußfolgerungen machen kann, [die über das bloß Denkmögliche hinausreichen]. Zunächst handelt es sich um einfache Dinge, die aber schon komplizierter werden, wenn man zum Begriff der vierten Dimension kommen will. Wir müssen uns klar darüber werden, was wir unter Dimensionen verstehen. Am besten macht man es sich klar, wenn man die verschiedenen Raumgebilde auf ihre Dimensionalität hin prüft. Sie führen zu Betrachtungen, welche erst im 19. Jahrhundert von großen Mathematikern wie Bolyai, Gauß und Riemann in Angriff genommen worden sind.1Note
Die einfachste Raumgröße ist der Punkt. Er hat gar keine Ausdehnung; er muß gedacht werden. Er ist die Fixierung einer Ausdehnung im Raume. Er hat keine Dimension. Die erste Dimension ist die Linie. Die gerade Linie hat eine Dimension, die Länge. Wenn wir die Linie, die keine Dicke hat, selbst bewegen, treten wir aus der einen Dimension heraus, und die Linie wird zur Fläche. Diese hat zwei Dimensionen, eine Länge und eine Breite, Wenn wir die Fläche bewegen, so treten wir aus diesen zwei Dimensionen heraus, und wir erhalten den Körper. Er hat drei Dimensionen: Höhe, Breite, Tiefe (Figur 1).

Wenn Sie den Körper selbst bewegen, wenn man [zum Beispiel] einen Würfel im Raume herumführt, werden Sie wiederum nur einen Raumkörper bekommen. Sie können den [dreidimensionalen] Raum nicht aus sich heraus bewegen.

Wir müssen uns noch ein paar anderen Begriffen zuwenden. Wenn Sie eine gerade Linie betrachten, hat sie zwei Grenzen, zwei Endpunkte A und B (Figur 2).
Stellen wir uns vor, daß A und B sich berühren sollen. Wenn sie sich berühren sollen, müssen wir aber die Gerade krümmen. Was geschieht? Sie können unmöglich in der [eindimensionalen] Geraden drinnenbleiben, wenn Sie A und B zusammenfallen lassen wollen. Um die Punkte A und B zu verbinden, müssen wir aus der Geraden selbst heraustreten, müssen wir also aus der ersten Dimension heraus und übergehen in die zweite Dimension, die Fläche. Auf diese Weise entsteht aus der Geraden [eine geschlossene Kurve, das heißt im einfachsten Falle] ein Kreis, indem ihre Endpunkte zur Deckung gebracht werden (Figur 3).

Es ist also notwendig, aus der ersten Dimension herauszugehen, man kann nicht in ihr drinnenbleiben. Nur so entsteht der Kreis. Sie können dieselbe Operation mit einer [rechteckig begrenzten] Fläche machen. Dies geht aber nur, wenn Sie nicht in den zwei Dimensionen drinnenbleiben. Sie müssen in die dritte Dimension hineingehen und bekommen dann aus der Fläche eine Röhre, einen Zylinder. Diese Operation geschieht auf ganz entsprechende Weise wie vorher, wo wir zwei Punkte zur Deckung brachten und dabei aus der ersten Dimension herausgegangen sind. Wir müssen hier [bei der Fläche], um zwei Grenzen der Fläche zur Deckung zu bringen, in die dritte Dimension hinübergehen (Figur 4).

Ist es denkbar, daß mit einem Raumgebilde, das schon selbst drei Dimensionen hat, eine ähnliche Operation ausgeführt werden könnte? Wenn Sie zwei kongruente Würfel haben, können Sie den einen in den anderen schieben. [Denken Sie sich nun zwei kongruente Würfel als Begrenzungen eines dreidimensionalen prismatischen Körpers.] Wenn Sie versuchen, den einen Würfel, der auf einer Seite rot [und auf der gegenüberliegenden Seite blau] gefärbt ist, zur Deckung zu bringen mit dem anderen Würfel, der sonst [geometrisch] ganz gleich ist, aber bei dem die rote und blaue Farbe vertauscht sind, dann können Sie die Deckung nicht anders herbeiführen, als indem Sie den Würfel drehen (Figur 5).

Betrachten wir ein anderes Raumgebilde. Nehmen Sie den Handschuh der linken Hand, so ist es Ihnen unmöglich, den Handschuh der linken Hand über die rechte Hand zu ziehen. Wenn Sie aber die beiden [spiegelsymmetrischen] Handschuhe zusammengehend betrachten wie die gerade Linie mit den Endpunkten A und B, so haben Sie etwas Zusammengehöriges. Es handelt sich dann um ein einziges Gebilde, mit einer Grenze [das heißt mit einer Spiegelebene] in der Mitte. Ganz ähnlich ist es auch mit den zwei symmetrischen Hälften der menschlichen Außenhaut.2Note
Wie können wir nun zwei [spiegel]symmetrische dreidimensionale Gebilde zur Deckung bringen? Nur wenn wir über die dritte Dimension hinausgehen, wie früher über die erste und zweite. Wir können den rechten oder linken Handschuh auch über die linke beziehungsweise rechte Hand stülpen, wenn wir durch den vierdimensionalen Raum gehen.3Note
[Beim Aufbau der dritten Dimension (Tiefendimension) des Anschauungsraumes] bringen wir das Bild des rechten Auges zur Deckung mit dem des linken, stülpen es darüber.4Note
Wir betrachten nun ein Beispiel von Zöllner.5Note Wir haben hier einen Kreis und außerhalb desselben einen Punkt P. Wie können wir den Punkt P [in den Kreis] hineinbringen, ohne den Kreis zu durchkreuzen? Dies geht nicht, wenn wir innerhalb der Ebene bleiben. So wie man aus der zweiten Dimension in die dritte hinübergehen muß beim Übergang vom Quadrat zum Würfel, so müssen wir auch hier aus der zweiten Dimension hinausgehen. Bei einer Kugel gibt es ebenfalls keine Möglichkeit [in das Innere] hineinzugehen, ohne [die Kugeloberfläche zu durchstoßen oder] über die dritte Dimension hinauszugehen.6Note

Das sind Denkmöglichkeiten, die aber eine praktische Bedeutung haben für die Erkenntnislehre, [insbesondere für das Problem der Objektivität des Wahrnehmungsinhaltes]. Wenn wir uns klarmachen, wie man eigentlich wahrnimmt, werden wir zu folgender Anschauung kommen. Fragen wir uns zunächst: Wie erlangen wir durch die Sinne Kenntnisse von den Körpern? Wir sehen eine Farbe. Ohne Augen würden wir sie nicht wahrnehmen. Der Physiker sagt dann: Da draußen im Raum ist nicht das, was man Farbe nennt, sondern rein räumliche Bewegungsformen; die dringen durch unser Auge, werden vom Sehnerv aufgefangen, zum Gehirn fortgesetzt, und dort entsteht zum Beispiel das Rot. Man kann sich nun fragen: Ist das Rot auch vorhanden, wenn keine Empfindung da ist?
Das Rot könnte ohne Auge nicht wahrgenommen werden. Glockenläuten könnte ohne Ohr nicht wahrgenommen werden. Alle unsere Empfindungen hängen davon ab, daß Bewegungsformen umgewandelt werden durch unseren physisch-seelischen Apparat. Die Sache wird aber noch komplizierter, wenn wir uns fragen: Wo ist denn nun eigentlich das Rot, diese eigentümliche Qualität? Ist es am Körper? Ist es ein Schwingungsvorgang? Draußen ist ein Bewegungsvorgang, und der setzt sich fort bis ins Auge hinein, bis ins Gehirn selbst. Überall sind Schwingungs- [und Nerven] vorgänge, nirgends ist Rot. Auch wenn Sie das Auge untersuchen, Sie würden nirgends Rot finden. Draußen ist es nicht, aber auch nicht im Gehirn. Nur dann haben wir Rot, wenn wir uns selbst als Subjekt diesen Bewegungsvorgängen entgegenstellen. Haben wir also überhaupt keine Möglichkeit, davon zu reden, wie das Rot dem Auge, wie Cis dem Ohr entgegenkommt?
Die Frage ist, was ist diese innere [Vorstellung], wo entsteht sie? In der philosophischen Literatur des 19. Jahrhunderts werden Sie finden, daß diese Frage alles durchzieht. Vor allem Schopenhauer7Note hat die folgende Definition aufgestellt: Die Welt ist unsere Vorstellung. - Was bleibt dann aber noch für den äußeren Körper? [So wie eine Farbvorstellung durch Bewegungen «erzeugt» werden kann, so kann auch] Bewegung in unserem Innern entstehen durch etwas, was im Grunde nicht bewegt ist. Betrachten wir dazu zwölf Momentaufnahmen einer [sich bewegenden] Pferdefigur auf [der Innenseite] einer [Zylinder-]Fläche, [die mit zwölf feinen Schlitzen in den Zwischenräumen versehen ist. Wenn wir seitlich auf den sich drehenden Zylinder blicken,] dann werden wir den Eindruck haben, daß es immer dasselbe Pferd bleibt, und daß es nur die Füße bewegt.8Note Also kann auch [der Eindruck von] Bewegung durch unsere [Leibes-Organisation] entstehen, wenn etwas sich [in Wirklichkeit] überhaupt nicht bewegt. So kommen wir zu einer vollständigen Auflösung von dem, was wir Bewegung nennen.
Was ist dann aber Materie? Ziehen Sie von der Materie ab Farbenglanz, Bewegung [Gestalt und so weiter, also das durch die sinnliche Wahrnehmung Vermittelte], dann bleibt nichts übrig. Wenn wir schon die [durch Außenweltvorgänge im individuellen Bewußtsein hervorgerufenen sekundären, das heißt «subjektiven»] Empfindungen [Farbe, Ton, Wärme, Geschmack, Geruch] in unserem Innern zu suchen haben, so müssen wir auch [die primären, das heißt «objektiven» Empfindungen, Gestalt und Bewegung,] in unser Inneres versetzen, und damit verschwindet die Außenwelt vollständig. Daraus ergeben sich aber große Schwierigkeiten [für die Erkenntnislehre].9Note
Nehmen wir an, alles wäre draußen, wie kommen dann die Eigenschaften des Gegenstandes draußen in uns hinein? Wo ist nun der Punkt [wo das Äußere in das Innere übergeht]? Wenn wir alle [sinnlichen Wahrnehmungsinhalte] abziehen, so gibt es kein Draußen mehr. Auf diese Weise versetzt sich die Erkenntnistheorie in die Lage von Münchhausen, der sich am eigenen Haarschopf frei in die Höhe ziehen will.10Note Nur dann aber, wenn wir annehmen, daß es ein Draußen gibt, nur dann können wir zu [einer Erklärung der] Empfindungen drinnen kommen. Wie kann etwas von außen in unser Inneres hereinkommen und als unsere Vorstellung auftreten?
Wir müssen die Frage noch anders aufwerfen. Wir betrachten zuerst einige Analogien. Sie werden keine Möglichkeit haben, eine Beziehung [zwischen Außenwelt und Innenempfindung] zu finden, wenn Sie nicht zu folgendem greifen. Wir kehren zurück zur Betrachtung der geraden Linie mit den Endpunkten A und B. Wir müssen über die erste Dimension hinausgehen, die Linie krümmen, um die Endpunkte zur Deckung zu bringen (Figur 7).
Denken Sie sich nun den linken Endpunkt A [dieser geraden Linie] mit dem rechten Endpunkt B so zusammengebracht, daß sie sich unten berühren, so daß wir imstande sind, [über die zusammenfallenden Endpunkte hinweg] zum Ausgangspunkt zurückzukehren. Wenn die Linie klein ist, ist auch der entsprechende Kreis klein. Wenn ich die [zunächst gegebene] Linie zum Kreise mache und dann immer größere Linien zu Kreisen mache, dann rückt der Punkt, in welchem sich die Endpunkte treffen, immer weiter von der [ursprünglichen] Linie ab und geht in unendliche Entfernung.

der [ursprünglichen] Linie ab und geht in unendliche Entfernung. Erst in der unendlichen Entfernung haben [die größer werdenden] Kreislinien ihren Endpunkt. Die Krümmung wird dabei eine immer schwächere, und schließlich werden wir unmöglich mit dem gewöhnlichen Auge die Kreislinie von der Geraden unterscheiden können (Figur 8).

Ganz entsprechend erscheint uns auch die Erde als ein gerades [flaches] Stück, wenn wir auf ihr gehen, obgleich sie rund ist. Wenn wir uns denken, daß die beiden Hälften der geraden Linie bis in die Unendlichkeit ausgedehnt werden, fällt der Kreis wirklich mit der Geraden zusammen.11NoteText Dabei kann die gerade Linie als Kreis aufgefaßt werden, dessen Durchmesser unendlich ist. Jetzt können wir uns allerdings vorstellen, daß, wenn wir [die gerade Linie durchlaufen und dabei] in der Linie drinbleiben, wir von der anderen Seite aus der Unendlichkeit [wieder] zurückkommen. Dabei müssen wir aber durch die Unendlichkeit hindurchgehen.

Denken Sie sich nun statt einer [geometrischen] Linie etwas, was eine Wirklichkeit ist, was sich verbindet mit einer Wirklichkeit. Stellen wir uns vor, daß mit dem Fortschreiten des Punktes C [auf der Kreisperipherie] eine Abkühlung eintritt, daß der Punkt immer kälter und kälter wird, je mehr er sich [von seinem Ausgangsort] entfernt (Figur 9). Lassen wir den Punkt zunächst innerhalb der Kreislinie, und, indem er immer kälter wird, die untere Grenze A, B erreichen. Wenn er auf der anderen Seite zurückkehrt, nimmt die Temperatur wieder zu. Es tritt also auf dem Rückweg der zu dem Hinweg entgegengesetzte Zustand ein. Die Erwärmung nimmt zu, bis die Temperatur bei C wieder erreicht ist, von welcher wir ausgegangen sind. Wie ausgedehnt auch der Kreis sei, es ist immer derselbe Vorgang: ein Abfließen der Wärme und ein Heranfließen derselben. Denken wir uns das auch bei der [unendlich ausgedehnten geraden] Linie: Indem sich die Temperatur [auf der einen Seite immer mehr] verliert, kann sie auf der anderen Seite steigen. Wir haben hier einen Zustand, der sich auf einer Seite verliert, während er sich auf der anderen Seite wieder aufbaut.
So bringen wir Leben und Bewegung hinein in die Welt und nähern uns dem, was wir in einem höheren Sinne «Begreifen der Welt» nennen können. Wir haben hier zwei Zustände, die sich bedingen, die voneinander abhängig sind. Für alles aber, was Sie [sinnlich] beobachten können, hat der Vorgang, der, sagen wir, nach rechts verläuft, nichts zu tun mit dem, der von links zurückkommt, und doch bedingen sie sich gegenseitig.12NoteText
Wir vergleichen nun den Körper der Außenwelt mit dem Abkühlungszustand und im Gegensatz dazu unsere Innenempfindung mit dem Erwärmungszustand. [Obwohl Außenwelt und Innenempfindung nichts unmittelbar sinnlich Wahrnehmbares gemeinsam haben,] stehen sie in einem Verhältnis zueinander, bedingen sich gegenseitig [in analoger Weise, wie sich die oben geschilderten Prozesse bedingen]. Daraus ergibt sich ein Zusammenhang der Außenwelt [mit unserer Innenwelt], den wir unterstützen können durch ein Bild: [durch das Verhältnis von] Petschaft und Siegellack. Das Petschaft läßt einen genauen Abdruck, eine genaue Wiedergabe des Siegels im Siegellack zurück, ohne daß das Petschaft im Siegellack zurückbleibt [und ohne daß etwas Materielles vom Petschaft in den Siegellack übergeht]. Im Siegellack bleibt also eine getreue Wiedergabe des Siegels zurück. Ganz entsprechend ist es auch beim Zusammenhang von Außenwelt und Innenempfindungen. Nur das Wesentliche [überträgt sich]. Die eine Zustand[sform] bedingt die andere, wobei aber nichts [Materielles] übergeht.13NoteText
Wenn wir uns vorstellen, daß es sich so verhält mit [dem Zusammenhang zwischen der] Außenwelt und unseren Eindrücken, kommen wir zu folgendem. [Geometrische] Spiegelbilder im Raume verhalten sich so wie Handschuhe von der linken und der rechten Hand. [Um diese unmittelbar und kontinuierlich miteinander in Beziehung zu setzen,] müssen wir eine neue Dimension des Raumes zu Hilfe nehmen. [Nun verhalten sich Außenwelt und Inneneindruck analog wie geometrische Spiegelbilder, können folglich ebenso nur durch eine weitere Dimension unmittelbar miteinander in Verbindung gebracht werden.] Um nun eine Beziehung herzustellen zwischen Außenwelt und Inneneindrücken, müssen wir also durch eine vierte Dimension gehen, müssen wir in einem dritten Element sein. Nur dort können wir das Gemeinschaftliche [von Außenwelt und Inneneindrücken] suchen, wo wir [mit ihnen] eins sind. [Man kann sich diese Spiegelbilder wie] schwimmend in einem Meere [vorstellen], innerhalb welchem wir die Spiegelbilder zur Deckung bringen können. Und so kommen wir [zunächst rein gedanklich] zu etwas, was über den dreidimensionalen Raum hinweggeht und doch eine Wirklichkeit hat. Wir müssen also unsere Raumvorstellungen ins Leben bringen, sie beleben.
Oskar Simony14NoteText hat versucht, diese belebten Raumgebilde mit Modellen darzustellen. [Wie wir gesehen haben, kommt man] von der Betrachtung des Nulldimensionalen [schrittweise] zur Möglichkeit, sich den vierdimensionalen Raum vorzustellen. [Anhand der Betrachtung spiegelsymmetrischer Körper, das heißt mit Hilfe der] Symmetrieverhältnisse, können wir diesen Raum zuerst [am leichtesten] erkennen. [Ein anderes Mittel, die Besonderheiten des empirischen dreidimensionalen Raumes im Verhältnis zum vierdimensionalen Raum zu studieren, bieten die Verknotungen von Kurven und Bändern.] Was versteht man unter Symmetrieverhältnissen? Dadurch, daß wir Raumgebilde miteinander verschlingen, rufen wir bestimmte Komplikationen herbei. [Diese Komplikationen sind Besonderheiten des dreidimensionalen Raumes; sie kommen in vierdimensionalen Räumen nicht vor.15NoteText
Lassen Sie uns ein paar praktische Denkübungen machen. Wenn wir einen Bandring in der Mitte durchschneiden, erhalten wir zwei solche Ringe. Zerschneiden wir nun entsprechend ein Band, dessen Enden um 180° verdreht und dann verklebt worden sind, so erhalten wir einen einzigen verdrehten Ring, der nicht zerfällt. Verdrehen wir die Band-Enden um 360° vor dem Zusammenkleben, so ergeben sich beim Zerschneiden zwei ineinander verschlungene Ringe. Verdrehen wir schließlich die Band-Enden um 720°, so ergibt sich durch denselben Prozeß ein Knoten.16NoteText
Wer nachdenkt über Naturvorgänge, weiß, daß solche Windungen in der Natur vorkommen; [in der Wirklichkeit sind] solche verschlungenen Raumgebilde mit Kräften versehen. Nehmen Sie etwa die Bewegung der Erde um die Sonne, und dann die Bewegung des Mondes um die Erde. Man sagt, der Mond beschreibe um die Erde einen Kreis, doch [wenn man genauer hinsieht] ist es eine Linie, die wieder [um einen Kreis, den Bahnkreis der Erde,] herumgeschlungen ist, also eine Schraubenlinie um eine Kreislinie. Und dann haben wir die Sonne, die so schnell durch den Weltenraum eilt, daß der Mond noch um sie eine [zusätzliche] Schraubenbewegung macht. Es sind also sehr komplizierte Kräftelinien, die sich im Raume erstrecken. Wir müssen uns vergegenwärtigen, daß wir es mit komplizierten Raumbegriffen zu tun haben, die wir nur dann begreifen, wenn wir sie nicht starr werden lassen, wenn wir sie flüssig haben.
Vergegenwärtigen wir uns das Gesagte noch einmal: Das Nulldimensionale ist der Punkt, das Eindimensionale ist die Linie, das Zweidimensionale die Fläche und das Dreidimensionale der Körper. Wie verhalten sich diese Raumbegriffe zueinander?
Denken Sie sich, Sie wären ein Wesen, welches überhaupt nur längs einer geraden Linie sich bewegen kann. Wie müßten die Raumvorstellungen von solchen Wesen geartet sein, die selber nur eindimensional sind? Sie würden die Eindimensionalität bei sich nicht wahrnehmen, sondern nur Punkte sich vorstellen. Denn es gibt in der geraden Linie, wenn wir in ihr etwas zeichnen wollen, nur Punkte, Ein zweidimensionales Wesen könnte Linien antreffen, also eindimensionale Wesen unterscheiden. Ein dreidimensionales Wesen, etwa der Würfel, würde die zweidimensionalen Wesen wahrnehmen. Der Mensch nun kann drei Dimensionen wahrnehmen. Wenn wir richtig folgern, müssen wir uns sagen: Wie ein eindimensionales Wesen nur Punkte wahrnehmen kann, wie ein zweidimensionales Wesen nur eine Dimension, und ein dreidimensionales Wesen nur zwei Dimensionen wahrnehmen kann, so kann ein Wesen, das drei Dimensionen wahrnimmt, nur ein vierdimensionales Wesen sein. Dadurch, daß ein Mensch äußere Wesen nach drei Dimensionen abgrenzen kann, mit Räumen aus drei Dimensionen [umgehen kann], muß er vierdimensional sein.17NoteText Und ebenso wie ein Würfel nur zwei Dimensionen wahrnehmen kann und nicht seine dritte, so ist es wahr, daß der Mensch die vierte Dimension, in der er lebt, nicht wahrnehmen kann.

