Notes from Mathilde Scholl 1904–1906
GA 91
4 November 1904, Berlin
Translated by Steiner Online Library
3. Trigonometry
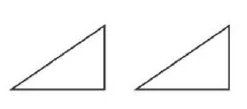
Triangles that can be superimposed exactly on top of each other are called congruent. If they cannot be superimposed exactly on top of each other, but can be superimposed in such a way that one can be placed on top of the other, but not of the same size, they are called similar if the third lines are parallel and partially overlap.
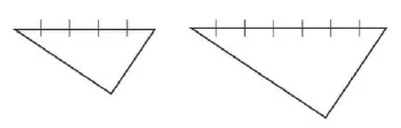
One side five units long. One side seven units long.
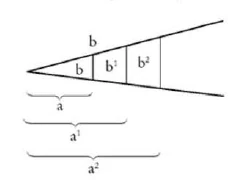
To get a similar triangle, I connect the third point and the fifth point, then I get two parallel lines.
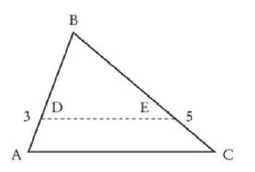
Two triangles are similar if they can be superimposed on each other, coinciding at an angle and with two sides parallel.
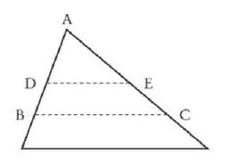
Two triangles are similar if they have the same angles. In similar triangles, the sides opposite the same angle are in the same proportions.
\(2:5 = 4:10\) is a proportion
\(a:b = c:d\)
If you multiply the two outer or the two inner terms, you get the same product: Then \(a \times d = b \times c\).
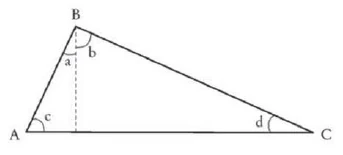
\(a + b = 90°\)
\(c + d = 90°\)
\(d + b = 90°\)
\(c + a = 90°\)
The square of the perpendicular is equal to the product of the two parts of the hypotenuse.
\(ABD ~ BDC\)
\(AD:BD = BD:DC\)
\(BD \times BD =AD \times DC\)
\(P^2 = d \times D\)
\(P^2 = d' \times D'\)
You can cross the diameter on the circumference three times and then there is a remainder, this remainder is approximately \(\frac{1}{7}\) of the diameter. So the circumference of the circle is \(3 \frac{1}{7}\) times the diameter.
\(U = 3 \frac{1}{7}\)
\(U = 3,14159[D] = \pi[D]\)
3. Dreiecksgeometrie

Dreiecke, die sich genau übereinanderlegen lassen, nennt man kongruent. Wenn sie sich nicht genau übereinanderlegen lassen, sondern sich so verhalten, dass man eins auf das andere legen kann, aber nicht gleich groß, heißen sie ähnlich, wenn die dritten Linien parallel sind und sich teilweise decken.

Eine Seite fünf Einheiten lang. Eine Seite sieben Einheiten lang.
Um ein ähnliches Dreieck zu bekommen, verbinde ich den dritten Punkt und den fünften Punkt, dann bekomme ich zwei parallele Linien.

Zwei Dreiecke sind ähnlich, wenn sie übereinander gelegt sich so decken, dass sie in einem Winkel sich decken und zwei Seiten parallel laufen.

Zwei Dreiecke sind ähnlich, wenn sie alle Winkel gleich haben. Bei ähnlichen Dreiecken sind die dem gleichen Winkel gegenüberliegenden Seiten in den gleichen Verhältnissen.
\(2:5 = 4:10\) eine Proportion
\(a:b = c:d\)
Wenn man die zwei äußeren Glieder oder die zwei inneren Glieder multipliziert, so bekommt man das gleiche Produkt: Dann ist \(a \times d = b \times c\).

\(a + b = 90°\)
\(c + d = 90°\)
\(d + b = 90°\)
\(c + a = 90°\)
Das Quadrat des Lots ist gleich dem Produkt aus den zwei Teilen der Hypotenuse.
\(ABD ~ BDC\)
\(AD:BD = BD:DC\)
\(BD \times BD =AD \times DC\)
\(P^2 = d \times D\)
\(P^2 = d' \times D'\)


Man kann den Durchmesser auf dem Umfang dreimal hinüberlegen und dann bleibt ein Rest, dieser Rest geht ungefähr \(\frac{1}{7}\) vom Durchmesser. Also der Umfang des Kreises ist \(3 \frac{1}{7}\)-mal so groß wie der Durchmesser.
\(U = 3 \frac{1}{7}\)
\(U = 3,14159[D] = \pi[D]\)

